fixed points in data

For far too long now, whenever someone shares my “graphics matter” series of posts, someone pipes up with a response that can be summarized as:

“We don’t know how many firearms there are in America, so we cannot draw any correlation or causation conclusions between firearms and the people they kill.”

It is time I address this notion.

The first phrase of the sentence is actually correct.  Not only are firearms a durable good – meaning that firearms produced before the Revolutionary War could still be used today so long as they were properly maintained – but national registration of non-NFA-regulated firearms is outlawed by the Firearm Owners Protection Act.

As well it should be – the government simply has no business knowing what I own.

“But that means the second phrase of the sentence has to be correct, right?”

Well, no.

The entire point of the “graphics matter” series is to examine the correlation of the number of firearms in America with the number of firearm-related fatalities or crimes in America, as well as the per-population rate of the same.  The fun thing about correlating two data sets is that you do not need to know their starting points.

“Wait, what?”

It is one of the fundamental aspects of correlation, really. “Positive correlation” means that “as data set A increases, data set B also increases”. “Negative correlation” means that “as data set A increases, data set B also decreases”.

(An important distinction I want to make before moving on is that this does not mean A’s increase causes B’s increase, or vice versa, or anything of the sort.  The world is full of correlations that have no causal relationship with one another.)

The reason the definitions are significant is this – you are looking at the rate of change. The “slope”, for those of you who remember… what was that, high school algebra?

But rate of change – slope – is determined between two points, and is completely independent of Y-intercept, or any starting point. As long as point 1 is separate from point 2 by the expected difference, it doesn’t actually matter what the individual values are.

In other words, the slope between the X/Y data points of 1/100 and 2/200, and the slope between the X/Y data points of 1/0 and 2/100 are exactly the same, despite the values being different.

It is kind of whacky to think about, but in most-basic terms, 2x+10 has the same slope as 2x+100, but entirely different values, and both correlate against 4x in exactly the same way (they both have a correlation value of 1 with respect to 4x).

In fact, since this is a graphically-related site, let us look at an example.

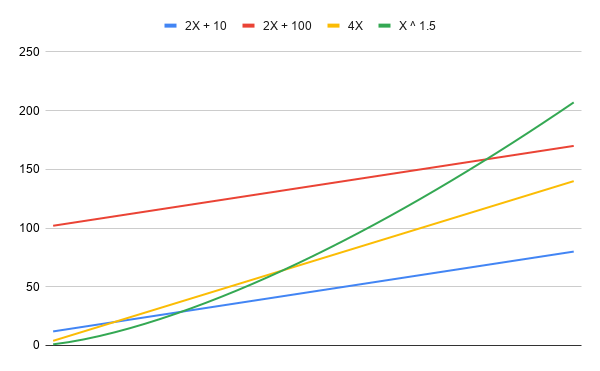
Here we have a plot of 2X + 10, 2X + 100, 4X, and X raised to the power of 1.5 over time.

As I mentioned above, both 2X + 10 and 2X + 100 correlate to 4X with a coefficient of 1, meaning that as the first two equations increase, the third equation also increases, and the ratio of the increases is always the same.  This makes sense – all three are straight lines, meaning their slope is constant along their lengths, so comparisons between those slopes will always be equal.

However, both of the first two equations correlate with X^1.5 with a coefficient of 0.99052.  Why?  Well, the slope of the fourth equation changes over time, since it involves a power.  The first two equations do not have the pronounced curve of the fourth, so their growth does not mirror the fourth’s growth, no matter how different that growth might be (as when comparing the first two equations with the third).  However, all three equations are increasing over time, hence their very strong correlation (coefficients can range from 1 to -1).

But the point – that I am perhaps belaboring – is that the first two equations have the exact same correlation with any other equation or line you care to throw on the chart with them.

Why does this matter?

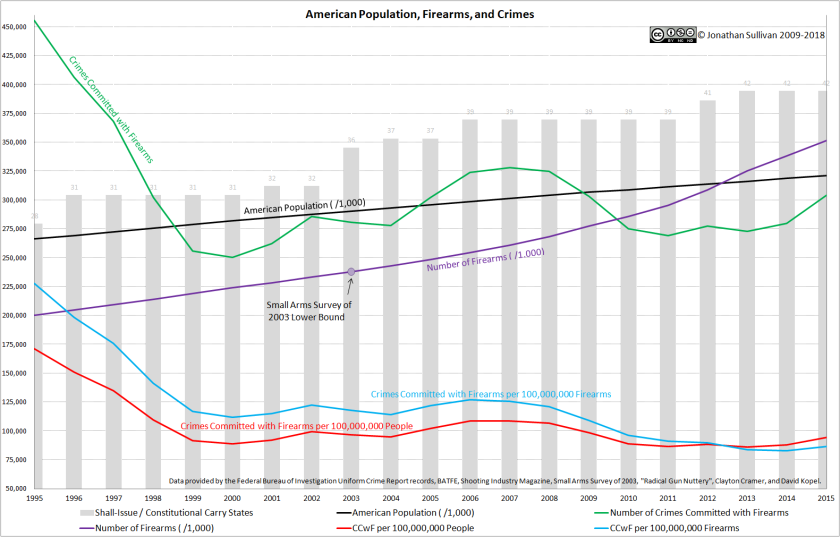
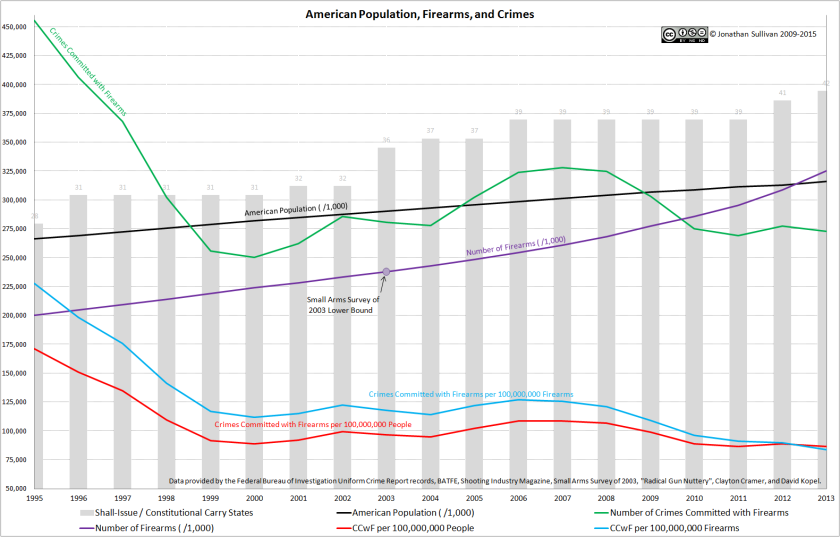
We really do not have any idea how many firearms are in America.  We never will.  I use the 2003 Small Arms Survey as the basis for my “graphics matter” series because it was the most-current when I started the post series, and changing reference points midway through is generally bad.

But I literally could have started in 1981 with the (atrociously flawed) assumption that there were no firearms in America, and the math would still work out exactly the same.

“Uh… why?”

We will never know how many firearms there are in America at any given time, but we do have a very accurate accounting of how many firearms are produced and imported into the country every year.  The BATFE’s Firearms Commerce in the United States Annual Statistical Update provides us that data back to 1986, and then the Shooting Industry News covers the remainder.  How can this be so accurate?  National registries may be outlawed, but all new firearms commercially produced must be uniquely serialized, and must be declared to the BATFE at the end of the year.  The penalties for “fudging” numbers are… severe.

We have the yearly production data.  Which means we have the rate of change – the slope.

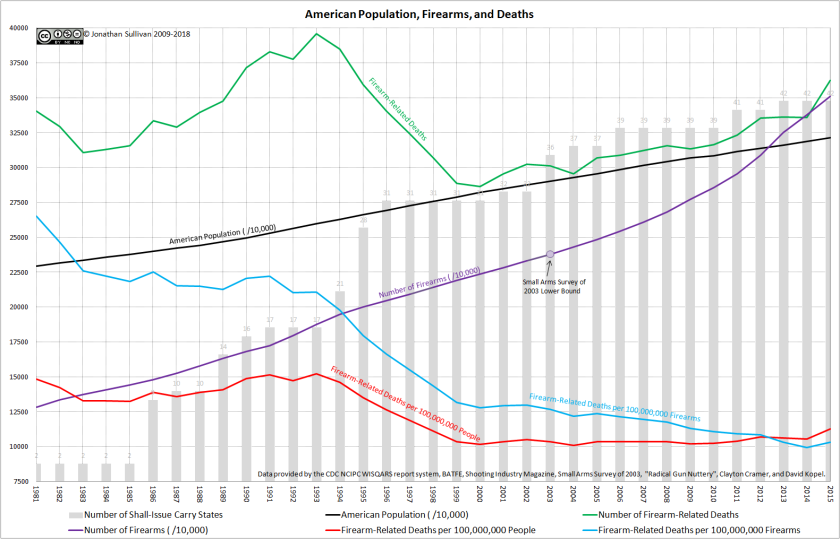
Likewise, we have a… noticeably less-accurate, but still-considered-reliable accounting of the American population and the number of Americans who were killed by other people using firearms at the CDC WISQARS Fatal Injury Report.  I refer to this as “less-accurate”, because I have personally witnessed the CDC correcting data five years past; while I would prefer accurate data over leaving the inaccurate data, it annoys me that, for example, they got the American population wrong by 300,000 residents in one year.

Having to go back and update my data aside, we have the yearly numbers of firearm-related fatalities, which means we can calculate the rate of change.

In other words, I – or you – can compare the two-year-paired slopes for each of those data sets, or the average slope as a whole, or any other combination, and it simply does not matter where the firearms data started.  Only the differences between each year’s data matters, and we have those differences tallied by “authoritative” sources.

Feel free to play with the situation yourself; I have uploaded the spreadsheet for the above graphic, and you can fiddle with the numbers to see how things change.

We genuinely have no idea how many firearms there are in America, and that is fine.  We do know how many have been produced a year for the past ~35 years, and the only correlation between the change in firearms in America and the change in firearm-related fatalities is negative-to-non-existent, for both raw numbers and per-American rates.  Thus, “more guns = more deaths” cannot be true.

graphics matter, 2019 edition

Honestly?  I’m tired of writing these posts.  Because reality does not change.

No matter the “gun control” extremists’ beliefs, inanimate objects cannot control a human being’s behavior.

To believe otherwise is pure fetishism.

But people continue to believe otherwise, so here we are.

As always, check out the original version of this post for the series’ explanation.  And, as always, “more guns = more deaths” is not my hypothesis, nor does this series of posts mean to prove that “more guns = fewer deaths”.

Instead, this series of posts exclusively exists to disprove the notion that more firearms automatically means more fatalities, as the aforementioned “gun control” extremists incessantly, erroneously declare.

My sources include:

– the CDC WISQARS Fatal Injrury Report
– the BATFE Firearms Commerce in the United States Annual Statistical Update 2018
– the Small Arms Survey of 2003
– Radical Gun Nuttery
– my data spreadsheet

And, once again, as every time previous, the hypothesis of “more guns = more deaths” falls flat on its face.

Now, it’s absolutely worth noting that the firearm-related fatalities are almost as high as their peak back in the early ’90s… but the US population has grown massively since then, meaning the rate of firearm-related fatalities is actually down since then.

Relatedly – pun intended – the correlation between the raw number of firearms in the United States and the raw number of firearm-related fatalities in the United States is -0.03268.

That is to say, there is precisely no correlation.

Which means there cannot be causation.

And that is a complicated way of saying, “the number of firearms in America is not driving the number of firearm-related deaths in America.”

Which brings us to rates, and any sociologist knows that rates are much more valuable than raw numbers.

Well, the correlation between the rate of firearm ownership – that is to say, the number of firearms in America divided by the American population – and the rate of firearm-related fatalities is -0.34575.

In other words, there is a noticeable, negative correlation.

Which, again, means there cannot be causation.

Look, I get it.

Kind of.

It is literally an article of faith among some people that “guns are bad”.

But the data simply does not back that prejudice up.  And, frankly, it is kind of disappointing that modern people are still bitterly clinging to the notion that inanimate lumps of metal can affect conscious, cognizant humans’ minds.

But here we are.

graphics matter, part two, 2018 edition

The first version of this post (on this site, at least) provides the full explanation of how and why this series exists, but the same two disclaimers from the first part of this year’s edition apply to this one as well:  “more guns = more ‘gun violence'” is not my hypothesis, and I am not setting out to prove causation.

As with last year’s update, I am using the usual sources:  the FBI’s Uniform Crime Report for 2015, the Centers for Disease Control, the Small Arms Survey of 2003, the BATFE’s Firearms Commerce in the United States, and Radical Gun Nuttery.

So, have the “gun control” extremists’ pipe dream of “more guns = more ‘gun violence'” finally come true?

You probably already know the answer.

The rate of average firearm ownership in America and the rate of crimes committed with firearms correlates with a coefficient of -0.734, indicating a strong, negative correlation between the two.

The raw number of firearms in America and the raw number of crimes committed with firearms correlates with a coefficient of -0.40019, indicating a negative correlation between the two.

In other words, the hypothesis of “more guns = more ‘gun violence’ remains false.  Still.

(Feel free to check my work (*.xlsx file).)

(Important note:  It has come to my attention that comparing, for example, this year’s correlation numbers to last year’s correlation numbers will be inherently flawed, on account of both the FBI and the CDC going back and updating/correcting/etc. information up to five years in the past.  The most-recent “graphics matter” post will have the most-recent information from both sources, but the previous years’ information from last year’s posts may have been updated/changed.  I do not know how, for example, the CDC managed to misrecord the US population from four years ago, but it is a little annoying.)

graphics matter, 2018 edition

Before I provide you this year’s update on the data, it has come to my attention that I need to clarify a few things.

1. The hypothesis of “more guns = more deaths” is not my hypothesis, claim, or allegation.  In point of fact, it is the underlying, foundational argument of every “gun control” organization in the country, and I am simply accepting it, at face value, for the sake of examining it.
2. I am not setting out to prove any causation.  In other words, I am emphatically not making the counter-argument that “more guns = fewer deaths”.  Such a claim would require a lot more work and study than I am willing to put into these posts, unlike those aforementioned “gun control” organizations, who are more than willing to perpetuate easily-believable falsehoods in order to line their pockets and unjustly limit your rights.

With those caveats made as explicit as I can, it’s time to give y’all the update to last year’s post.  So, with another year’s data under our belt, is the hypothesis of “more guns = more deaths” accurate?

… not so much.

There was a surprising uptick in firearm-related fatalities in 2015, but over the course of the 34 years tracked, the trend remains mostly the same.

The number of firearms per capita and the number of firearm-related fatalities per capita correlate with a coefficient of -0.74808 – indicating a very strong, but negative, correlation between the two data sets.

The number of total firearms and the number of total firearm-related fatalities correlate with a coefficient of -0.17420 – indicating a significantly weaker, but still negative, correlation.

As students of statistics remember, correlation does not prove, or even indicate, causation, but correlation is a requirement for causation.  In other words, given that neither the rates nor the raw numbers are positively correlated, then the increase in firearms in the country over time cannot be causing an associated increase in firearm-related deaths.

In simpler terms, the hypothesis of “more guns = more deaths” remains false.

(The first post in this series, wherein I spell out the above caveats differently, but I thought fairly clearly, is available here.  The source Excel spreadsheet from which I generated the above graphic and numbers is available here, should anyone care to check my work.  As always, my sources are the CDC’s WISQARS Fatal Injury Reports (for firearm-related deaths and the US population), the Small Arms Survey of 2003 (for a starting point from which to calculate the number of firearms in circulation), the BATFE’s Firearms Commerce in the United States (this time the 2017 edition, and for the number of firearms produced/imported), the Shooting Industry News (for firearm production numbers before 1986), and Radical Gun Nuttery (for the number of shall-issue/Constitutional Carry states in the Union).

graphics matter, part two, 2017 edition

Last year’s edition of this post adequately explained the methods and reasons behind this post, so feel free to skim it if you need a refresher.  The sources remain the same:

• FBI’s Uniform Crime Reports for 2014 (documenting, well, crime)
• Centers for Disease Control (providing the population of the US)
• Small Arms Survey of 2003 (I use their 2003 estimate as the start-point for my estimation of the total firearms in the US)
• BATFE’s Firearms Commerce in the United States (predictably, they track the number of firearms manufactured or imported into the US)
• Radical Gun Nuttery (despite the site’s name, they keep an accurate count of May-Issue/Shall-Issue/Constitutional-Carry states)

So, with another year of data under our belt, does my answer to the hypothesis of “more guns = more ‘gun violence’” change?

Nope.

The short answer is that the rate of firearm ownership correlates with the rate of crimes committed with a firearm with a coefficient of -0.57582, showing a negative correlation between the two.

Likewise, the raw number of firearms in private hands correlates to the raw number of crimes committed with a firearm with a coefficient of -0.44568, also indicating a negative correlation between these two data sets.

In a shock to no one, the hypothesis of “more guns = more ‘gun violence'” still cannot be true.

As always, please feel free to check my work (*.xlsx file).

 

graphics matter, 2017 edition

“More data more better” is pretty much the rule when it comes to statistics, so I try to update the “graphics matter” series every year or so as my various sources update their data sets.  I missed a year somewhere in there, but I am happy to bring you the new, improved, examination of whether or not the hypothesis of “more guns = more ‘gun deaths'” holds true.

The results… will not surprise regular readers.

That is the chart, but what about the actual numbers?

The two pertinent rates – the number of firearms per capita versus the number of firearm-related fatalities per capita – correlate with a coefficient of -0.79744, indicating a strong, negative correlation between the two sets of data.

If you look at the raw numbers – the number of firearms, period, versus the number of firearm-related fatalities, or “gun deaths” – they correlate with a coefficient of -0.27315, which remains a negative correlation.

As always, correlation does not necessarily indicate, or even come close to proving, causality; but I am also not trying to prove causality.  However, the notion of “more guns = more ‘gun deaths'” does try to claim causality, when there is absolutely no positive correlation to support such a causal link.

Therefore, the hypothesis of “more guns = more ‘gun deaths'” still cannot be true.

(The previous version of this, along with a great deal more explanation, is available here.  The Excel spreadsheet from which I built the above graphic is available here.  My sources are the CDC’s WISQARS Fatal Injury Reports, the Small Arms Survey of 2003, the BATFE’s Firearms Commerce in the United States, the Shooting Industry News, and Radical Gun Nuttery.)

graphics matter, part three

As previously demonstrated, the hypothesis of “more guns = more deaths” not only is not true, but cannot be true historically in the United States.  Despite that simple fact, “gun control” supporters still bitterly cling to the irrational notion that firearms are naught but the tools of murder and mayhem.

So let us humor them for a second.  We know that the number of firearms in circulation in America has been steadily increasing for as long as the Bureau of Alcohol, Tobacco, Firearms, and Explosives has been tracking the relevant numbers.  Likewise, the raw murder count in the States has dropped to numbers unseen since the 1960s.

However, what about the percentage of those murders committed with the assistance of a firearm?  After all, if firearms’ only purpose is to murder other people, one would think that, even if the overall murder rate is going down, the percentage of murders that involved a firearm would be going up given the increased number of firearms in the country.

Right?

Well, as with many of the things “gun control” advocates purport to be “common sense”, the reality is a little more complicated:

The grey bars track the percentage of murders that were committed with the assistance of a firearm, and, as you can see, those bars do not come anywhere close to echoing the consistent climb of the number of firearms in the United States.

In fact, the trend line for the percentages is functionally level, with a slope of 0.0006, compared to the slope of 669.64 for the number of firearms in America.  Oh, and yes, that does mean that, averaged over the past 20 years, at least 6,696,400 firearms have been produced in or imported into the United States every year.

Despite the nearly level trend line of the percentages, there does exist a correlation of 0.14784 between the number of firearms in the United States and the percentage of murders committed with the assistance of firearms.  This is, however, a tremendously weak correlation, and given the very narrow range of percentages – a maximum of 64% and a minimum of 55% – it is certainly not enough to draw any kind of causal relationship.

So, could the increased number of firearms in public circulation lead to a higher percentage of murders involving those firearms?  Based on the available data, yes, it is possible… but it has not been happening consistently yet.

Source *.xls file.

Other Sources:

Small Arms Survey of 2003

Shooting Industry News

graphics matter, international edition

Now that we have shown that the hypothesis “more guns = more ‘gun deaths'” cannot be true in America, what about on an international scale?

Well, this is where things get really complicated.

Not all countries keep good records of their respective murders, much less their respective firearm ownership, so we are going to have to do a massive amount of estimating.

For the number of firearms in civilian ownership, we will refer to the 2007 Small Arms Survey, Chapter 2, Annexe 3 (*.pdf warning) and their documentation of 178 different countries.  We will consider the numbers from every possible country in North, South, and Central America; North, South, Eastern, and Western Europe; Oceania; and a few other odds and ends to round out the data set to a good sample body of 100.  I used the average of the “Low Total from Outside Sources” and “High Total from Outside Sources” where available, and “Registered” if not, to generate the ownership numbers for the individual countries.  It is worth noting that some useful countries – like Denmark, India, and Luxembourg – are omitted from the survey; for these countries, the only numbers available are “Total from Regional Correlation” – i.e. they were making a guess based on the guesses they made around that country.

Likewise, the population numbers for the countries considered came from the same Small Arms Survey.

I hate to admit this, simply because I hate using Wikipedia as a primary source for anything, but the numbers of murders per country, from which I calculated their murder rates, is from the List of countries by intentional homicide rates.  As always, these numbers are subject to the inherent flaws in various countries’ recording methods, as well as the flaws intrinsic to Wikipedia itself.

It is worth noting that we are considering total murders this time around, rather than simply “gun deaths”.  If you think recording methods are inconsistent among various nations, just imagine how messy trying to track means of death would be.

Here is the end result:

You almost certainly will want to click on it to make it larger.

The line slanting down from left to right is the trendline of the datapoints; basically it shows that the correlation between firearm ownership rates and murder rates in the 100 countries sampled is negative, at a coefficient of -0.1832.  Note that this is a weak correlation, and thus cannot be considered binding.

In other words, as with the trend here in America, the hypothesis that “more guns = more deaths” cannot be true on an international scale.  I am not a betting man, but I am starting to see a trend here…

If you want to see what the other 100 countries were, since a goodly number are stacked on top of each other, the source data is available for your consideration.

graphics matter, part two

Now that we have dispensed with the myth that “more guns = more gun deaths”, what about the second-most-favorite talking point of the “gun control” movement: “more guns = more ‘gun violence’“?

Well, the first problem is what, exactly, is “gun violence”?  For simplicity’s sake, and for the sake of actually finding relevant data, I am going to define “gun violence” as “any crime committed with the assistance of a firearm”, or “CCwF” for short.  Specifically, after consulting the Federal Bureau of Investigation‘s Uniform Crime Reports for 2013, we are going to consider murders, robberies, and assaults where the perpetrators employed a firearm.

As with the previous post, the Centers for Disease Control will be providing the population of the United States (though we will not be using WISQARS, since we are not interested exclusively in fatalities or injuries), the Small Arms Survey of 2003 will provide the starting point of our firearm count estimation, with the Bureau of Alcohol, Tobacco, Firearms, and Explosives and Shooting Industry News providing the production numbers, and Radical Gun Nuttery did the counting for the number of “shall-issue” / “Constitutional carry” states out there.

So, given all of those wonderful numbers, do more guns really mean more “gun violence”?

Nope.

For the numerically inclined, the rate of firearm ownership correlates with the rate of crimes committed with firearms with a coefficient of -0.58535, indicating a negative correlation between the two data sets.

Even when we consider raw numbers, the number of firearms in America versus the number of crimes committed with firearms correlates with a coefficient of -0.46199, still indicating a negative correlation.

In other words, the hypothesis of “more guns = more ‘gun violence'” cannot be true.

Again, feel free to check my work (*.xlsx file); folks have pointed out mistakes I have made in the past, and I am always seeking greater accuracy.

Also, it is worth noting that somewhere in the 2012 to 2013 range, assuming the Small Arms Survey of 2003 is even close to accurate, America reached parity between its population and the number of firearms in its borders; there are enough firearms for every single American to own one.  I dare say our Founding Fathers would approve.

graphics matter

One of the favorite myths of “gun control” advocates is that as the number of firearms in Americans’ hands increases, so too does the number of firearm-related deaths increase.  Superficially, this seems to make sense, and thus it is an appealing fiction to buy into.

Fortunately, the actual data proves the hypothesis to be false.

To begin with, I should clarify that we will be considering the rates of firearm ownership and rates of firearm-related fatalities, since raw numbers are affected by population growth or decline.  Thankfully, the United States population is fairly well documented, and we will be using the Centers for Disease Control‘s information.

Additionally, causes of death are also well documented, also by the CDC.  Their WISQARS Fatal Injury Reports are updated on a yearly basis, and their data set spans from 1981 to 2012, so that will be our consideration window.

Unfortunately (from the analytical standpoint), the first part of the equation – the number of firearms in private Americans’ hands – is nowhere near as accurately recorded.  Obviously I am quite sanguine with the federal government having no idea who owns what firearms or in what numbers, but it does make statistical examinations a little more challenging.  However, the Small Arms Survey of 2003 is perhaps an authoritative estimate on private ownership of arms in various nations, and they calculate the lower bound of US firearm numbers in 2003 as approximately 238,000,000.  The Small Arms Survey organization is decidedly against the “proliferation of small arms”, by their own words, so we have every reason to believe they inflate their numbers for greater impact, but we can accept that as a starting point.

From that starting point, we will add, or subtract, the firearm production figures provided by the Bureau of Alcohol, Tobacco, Firearms and Explosives‘ Firearms Commerce in the United States document, at least as far back as 1986 (the earliest publication of that document).  Before then, we will rely on the Shooting Industry News.

Finally, while it does not factor into the “does ‘more firearms’ mean ‘more firearm-related deaths?” question, the number of “shall-issue” and “Constitutional carry” states is also included in the data, with the tallying done by Radical Gun Nuttery (their *.gif documenting the march of our rights across the nation is quite handy).

So, with all this data at our fingertips, does “more firearms = more firearm-related deaths” hold true?

In short, no.

For those who want more than pretty pictures, when one considers the rates – i.e. the number of firearms or firearm-related fatalities per 10,000 people – the rate of firearm ownership correlates to the rate of firearm-related fatalities with a coefficient of -0.80155, indicating a strong, negative correlation between the two data sets.

Even when you look at the raw numbers, the number of firearms in America correlated to the number of firearm-related fatalities – i.e. “gun deaths” – with a coefficient of –0.36471, which still indicates a negative correlation between those two data sets.

At this point, it is important to clarify that correlation does not indicate, nor prove, causality… but I am not attempting to prove causality here.  However, by stating that “more guns causes more ‘gun deaths'”, the anti-rights community is attempting to claim causality, and one that would outright require positive correlation.

No such positive correlation exists.

As such, the hypothesis of “more guns = more ‘gun deaths'” cannot be true.

Feel free to spread this information as far as you like, and if you are so inclined, I welcome people checking my work (*.xlsx file).  Unlike anti-firearms organizations, I make no attempt at hiding my raw data, or the ways it was crunched.

(As a further aside, it would not matter if the hypothesis could be true – the overwhelming majority of firearm-owning Americans have broken no laws nor harmed anyone, and, as such, no one has any standing to unjustly deprive them of property or rights.)